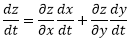Clase #23

Máximos y mínimos (o puntos extremos)

f: R2 → R

   (x,y)  → z=f(x,y)

Puede presentar:

1. Máximos o mínimos relativos (o locales)
2. Máximos o mínimos absolutos
3. Máximos o mínimos condicionados

Máximos o mínimos relativos (o locales)

Sea f: R2 → R una función de 2 variables esta tendrá

1. Máximo relativo en (a,b) si f(x,y) ≤ f(a,b) para todo (x,y) elemento de algún disco de centro (a,b).
2. Mínimo relativo en (a,b) si f(x,y) ≥ f(a,b) cuando (x,y) elemento está cerca de  (a,b).

Existen funciones que presentan un máximo y un mínimo a la vez en (a,b), entonces el punto (a,b) se denomina PUNTO DE SILLA.

Teorema

Si f tiene un máximo o mínimo relativo en (a,b) y las derivadas parciales de primer orden existen allí entonces:

f_x(a,b) = 0 ^  fy(a,b) = 0

El punto (a,b) se denomina PUNTO CRÍTICO (O ESTACIONARIO).

Prueba de la segunda derivada

Suponga que la segunda derivada parcial de f es continua en (a,b) y suponga que f_x(a,b) = 0 ^  fy(a,b) = 0 es decir (a,b) es un apunto critico de f entonces:

• Si D > 0 y f_xx(a,b) > 0 →  existe mR en (a,b)
• Si D > 0 y f_xx(a,b) < 0 →  existe  MR en (a,b)
• Si D < 0 →  existe  punto de silla en (a,b)
• Si D = 0 →  el criterio no define

Información adicional

Ejercicios sobre máximos y mínimos

Clase #22

Regla de la cadena

f: R2 → R

   (x,y)  → z=f(x,y)

x=x(t) y y=y(t)

z: var dependiente

x,y: var. Independientes

t: var. independiente

f: R2 → R

   (x,y,z)  → w=f(x,y,z)

x=h(u.v), y=g(u.v), z=l(u.v)

w: var dependiente

x,y,z: var. Independientes

u,v: var. independiente

Regla de la cadena general

f: Rm → R

   (x1,x2,x3,...,xm)  → u=f(x1,x2,x3,...,xm)

x1=x1(t), x2=x2(t), x3=x3(t),...,xm=xm(t)

u: var dependiente

(x1,x2,x3,...,xm): var. Independientes

t: var. independiente

Clase #21

Aproximaciones lineales

f: R3 → R

   (x,y,z)  → w=f(x,y,z)

Definición

Si z=f(x,y) entonces f es diferenciable en (a,b), ∆z se puede expresar de la forma

Donde ε1 y ε2 → 0 cuando (∆x, ∆y) → (0,0)

Teorema

Si las derivadas parciales fx ^ fy existen cerca de (a,b) y son continuas en (a,b) entonces f es diferenciable en (a,b)

Clase #20

Derivadas parciales de orden superior

En R3
f: R2 → R
   (x,y)  → z=f(x,y)

• Existen 4 derivadas parciales de orden 2.
• Existen 8 derivadas parciales de orden 3.
• Existen 2^n derivadas parciales de orden "n"
• Si tenenemos una f(x,y,z) existen 3^n derivadas parciales de orden "n"
• Si tenenemos una f(x1,x2, ... , xm) existen m^n derivadas parciales de orden "n"

Información adicional:

Clase #19

En esta clase se hizo una revisión del examen.

Clase #18

Planos tangentes a las superficies

Supongamos que f(x,y) tiene derivadas parciales continuas sobre un rectángulo en el plano xy que contiene a (a,b) en su interior. Entonces el plano tangente a la superficie z=f(x,y) en el punto P(a,b,f(a,b)) es el plano que pasa por P y que contiene a las rectas tangentes a las 2 curvas

z=f(x,b) ; y=b (curva x)

z=f(a,y) ; x=a (curva y)

La ecuación del plano tangente a z= f(x,y) en el punto P(a,b,f(a,b)) es

Derivada direccional

Por otro lado ahora se quiere evaluar que pasa con f(x,y) n la dirección del vector unitario arbitrario u=(a,b)

La derivada direccional de f en (xo,yo) en la dirección del vector unitario es

si existe el limite

Gradiente

Si f es una funcion de dos variables “x” y “y”, entonces el gradiente de f es la funcion vectorial ∇f definida por

Teorema

Si f es una funcion diferenciable de x y y entonces f tiene una derivada direccional en la dirección de cualquier vector unitario u=(a,b) y uf(x,y)=(fx(x,y)+fy(x,y))

• Si D_uf(x,y) es positivo entonces la funcion aumenta cuando se mueve a lo largo del vector unitario
• 
  
• Si D_uf(x,y) es negativo entonces la funcion disminuye cuando se mueve a lo largo del vector unitario.

Dirección de máximo crecimiento

Dirección de mínimo crecimiento

Nota: El vector gradiente siempre es proporcional al plano tangente en un punto.

Clase #17

Interpretación de las derivadas parciales

Percepción sobre el plano YOZ

Percepción sobre el plano XOZ

• Geométricamente las derivadas parciales de f(x,y) representan las pendientes de las rectas tangentes a las curvas C1 y C2.
• Las curvas C1 y C2 son las que se generan al intersecar la superficie z=f(x,y) con planos x=a y y=b respectivamente.
• Físicamente las derivadas parciales representan RAZONES o TASAS DE CAMBIO de f(x,y), cuando x o y se incrementan.

Nota: la palabra incremento se refiere a variación no solo a aumento.

Información adicional:

Clase #16

Derivadas parciales

En R³

f: R² ® R

   (x,y)  ® z=f(x,y)

x,y: variables independientes.

z: variable dependiente.

En R⁴

f: R³ ® R

   (x,y,z)  ® w=f(x,y,z)

x,y,z: variables independientes.

w: variable dependiente.

En Rⁿ

f: R^n-1 ® R

   (x1, x2, x3, ... , xn) ® u=f(x1, x2, x3, ... , xn) 

(x1, x2, x3, ... , xn) : variables independientes.

u: variable dependiente.

Información adicional:
Derivadas parciales

Clase #15

En esta fecha rendimos la segunda prueba.

Clase #14

• La intersección del plano z=k con la superficie z=f(x,y) se denomina CURVA DE CONTORNO de altura k sobre la superficie.
• La proyección de estas curvas de contorno en el plano XOY son las curvas de nivel f(x,y)=k de la función f.
• En un mapa topográfico, las curvas de nivel son curvas de altura constante sobre el nivel del mar.

• Si la f(x,y) representa la temperatura de una placa entonces f(x,y)=k representa las curvas de nivel que se denominan ISOTERMAS.
• Si la f(x,y) representa la presión de un gas, entonces las curvas de nivel se denominan ISOBARAS.
• Si la f(x,y) representa el potencial eléctrico, entonces las curvas de nivel se denominan CURVAS EQUIPOTENCIALES.

Límites y continuidad

En general:

• Existen ∞ curvas o trayecotiras de acercamiento a (a,b).
• Si por dos caminos el valor del limite es ≠ entonces concluimos que el limite no existe.
• Si por dos o mas caminos el valor del limite tiene igual valor, entonces suponemos que existe el limite y debemos proceder a demostrarlo.
• Para que f(x,y) sea continua en (a,b) se debe cumplir:

Esto implica que

Si una de estas consideraciones no se cumple se dice:

• f(x,y) es discontinua inevitable si 

• f(x,y) es discontinua evitable si

Bibliografía

Fuentes, E. (Abril de 2015). Monografias. Obtenido de http://www.monografias.com/trabajos87/informe-topografia/informe-topografia.shtml