Clase #13

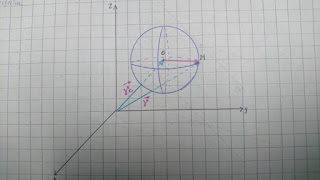
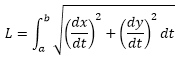Para representa la gráfica es una función f(x,y), se requiere de un sistema coordenado (x,y,z)(R³)

Definición

• Si f es una función de dos valriables con dominio D, entonces la grafica de f es el conjunto de todos los puntos (x,y,z) en R³, tal que z=f(x,y) está en D.
• La grafica de f(x,y) es una superficie en R³.

Ejemplo

Grafique la función:

f(x,y)= 6 -3x 2y

z= 6 -3x 2y

Curvas de nivel

Las curvas de nivel de una función f de dos variables son las curvas cuyas ecuaciones son f(x,y)=k, donde k es una constante (en el rango de f).

Ejemplo

Grafique las curvas de nivel de

f(x,y)= 6 -3x 2y

Por lo tanto las curvas de nivel son familia de rectas paralelas con pendiente negativa igual a -3/2.

Clase #12

Vectores normales y binomiales

Vector normal unitario:

Vector binormal unitario:

El triedro móvil se formaría:

Plano Osculador (PO)

Plano normal principal (PNP)

Plano rectificante (PR)

Recta tangente (RT)

Recta normal (RN)

Recta binormal (RB)

Ecuación radio de curvatura:

Funciones de varias variables

f: f: Rⁿ ® R

(x1, x2, x3, ... , xn) ® u=f(x1, x2, x3, ... , xn) 

Si n=2

f: f: R² ® R

(x,y)= z=f(x,y)

x,y: variables independientes.

z: variable dependiente.

Df={(x,y) € R² / z=f(x,y)}

Rf={z € R / z=f(x,y)}

Análisis del dominio de definición o dominio de existencia

Ejemplo:

1. Analíticamente

2. Gráficamente

3. Descriptivamente

 El dominio de la función son todos los pares ordenados (x,y) que se encuentran debajo de la recta y=-1-x, incluido el eje positivo de las "y" y parte del eje "x", no pertenece al dominio x=1.

Clase #11

Reparametrización

Toda curva alabeada C se representa por más de una función vectorial.

Ejemplo

r1(t)=(t ,t^2,t^3); 1 ≤ t ≤ 2

se puede representar por:

r2(t)=e^u,e^2u,e^3u; 0 ≤ u ≤ lu2

si t=e^u

• La longitud de arco es independiente de la reparametrización que se utilice.
• Suponga que C es una curva suave por partes dada por

r’(t) = f(t) i + g(t) j + h(t) k ; a ≤ t ≤ b

Donde r’(t) es continua y C es recorrida cuando t se incrementa desde “a” hasta “b”

Se define:

Siendo S(t) la longitud del arco de C entre r(a) y r(b)

Curvatura

• Una parametrizaciòn se dice suave en un intervalo I, si r’(t) es continua y r’(t) ≠ 0 en I.
• Una curva suave no tiene puntos agudo o cúspides, cuando gira el vector tangente, lo hace en forma continua.

Vector tangente unitario

El vector tangente unitario indica la dirección de la curva C.

Curvatura

La curvatura de C se define como

Pasos

Teorema

La curvatura de la curva C se calcula como:

Clase #10

Interpretación geométrica

Se puede considerar a F'(t) como el vector tangente a la curva c en el punto t.

Interpretación física

       1. F(t0) se considera el vector tangente a la curva c en to. F(to)=V(to),                vector velocidad ||F(to)|| representa la velocidad escalar

       2. El vector F’(to) cuando es diferente de cero determina la recta tangente            a la curva c

                 L{F(to) + tF(to); t € R}

                 R= Ro + ta

       3. Vector aceleración

       4. En R^3

                v(t) = ||V(t)|| =||F(t)||

           Es la rapidez de una partícula

Integración de funciones vectoriales

Propiedades

Longitud de arco y curva

En R^2

En R^3

Ecuación general de la curva

Clase #9

Operaciones con funciones vectoriales

Sean:

F; I→R^n  ^ G; I→R^n  h: J → I
donde I,J c R ^ u € R se define:

 f) (F o h)(t)=F(h(t))=(f1(h(t)),f2(h(t)), ... ,fn(h(t))) 

Ejemplo

Límites y continuidad

• Siempre que existan los límites de las funciones correspondientes.
• Los límites de las funciones vectoriales siguen las reglas y cumplen las mismas propiedades de los límites de las funciones reales escalares.

Una función R(t) es continua en a si:

• R(t) es continua en a, si solo si f(t), g(t), h(t) son continuas cuando t→a.
• Las propiedades de las operaciones con funciones reales escalares continuas se cumplen para las funciones reales vectoriales.

Derivación de funciones vectoriales

Dada la función vectorial F I→R^n, donde I c R, sea to € I, se dice que F(t) es derivable en to si existe

Si dicho límite existe, la derivada de F(t) en to se denota por:

• Para calcular la derivada de una función vectorial se debe derivar cada una de sus componentes.
• Se aplican las propiedades y reglas de derivación de las funciones reales escalares.

Información adicional:

Límites

Derivadas 1

Derivadas 2

Clase #8

Funciones vectoriales de variable real

Definición:

Se llama función vectorial de la variable real “t” a todas correspondencia de F de I c R en R^n

F: I → R^n

   t à F(t) = (f1(t), f2(t), … , fa(t))

Donde

fk (t) son funciones reales k=1,2,3,…, n

Dominio de F(t)

• Dom F(t)=Df1 ∩ Df2 …. ∩ Dfk

Rango de F(t)

• Rango F(t) =Rf1 U Rf2 … U Rfk

Ejemplo

Dom F(t) = R

Rango F(t)=R

• La gráfica de una función vectorial en R^3 es una CURVA ALAVEADA representada en el espacio.
• La gráfica de una función vectorial en R^2 es una CURVA PLANA representada en el plano XOY

Información adicional

Curva alaveada

Clase #7

En esta fecha rendimos la primera prueba.

Clase #6

Ejemplos del análisis gráfico de superficies

Ejercicio 1

Se trata de una elipsoide

Ejercicio 2

Se trata de un paraboloide hiperbólico (Silla de montar)

Clase #5

Recta determinada por dos planos

**Ecuación canónica de la recta L

 x-x0     =    y-y0   =    z-z0     
|B1 C1|     |C1 A1|    |A1 B1|
|B2 C2|     |C2 A2|    |A2 B2|

**Ecuación parametrica de la recta L    

x=x0 +  t |B1 C1|    
               |B2 C2|   
y=y0 +  t |C1 A1|    
               |C2 A2|   
z=z0 +  t |A1 B1|    
               |A2 B2|   

Ecuación del haz de planos

Haz de planos: conjunto de planos que pasa por la misma recta

A1x+A2 λx+B1y+B2 λy+C1z+C2 λz+D1+D2 λ=0
n=(A1+A2 λ; B1+B2λ; C1+C2 λ)

Ejercicio

Determinar el angulo entre los planos π1 y π2

Θ= arccos _______(A1.A2+B1.B2+C1.C2)______

               (√A1² + B1² + C1²).(√A2² + B2² + C2²)  

Ecuación de la superficie esférica

**Ec. de la superficie esférica con C(0,0,0) y r=R

(r-r0)=R^2 

**Ec. general de la superficie esférica con C(0,0,0) y r=R

(x-x0)^2 + (y-y0)^2 + (z-z0)^2)=R^2 

Caso particular:

Si C=(0,0,0) --> x^2+y^2+z^2=R^2

Ejercicio

Halle los vectores de los puntos de interseccion de la superficie esferica de ecuacion (R-R0)=R^2 y la recta r=ta.

r1= _____R_____(l,m,n)

      √l² + m² + n² 

r2= - _____R_____(l,m,n)

        √l² + m² + n² 

CILINDROS Y SUPERFICIES CUADRÁTICAS

Análisis gráfico de superficies

1. Intersección de la superficie con los ejes coordenados.
2. Intersección de la superficie con los planos coordenados
3. Intersección de la superficie con planos paralelos a los planos coordenados
4. Bosquejo de la gráfica de la superficie

Referencias:

* Apuntes del cuaderno

*https://sites.google.com/site/avcportafolio/_/rsrc/1427490715467/home/parcial-2/seccion-academica/Captura.JPG