Clase #5

Recta determinada por dos planos

**Ecuación canónica de la recta L

 x-x0     =    y-y0   =    z-z0     
|B1 C1|     |C1 A1|    |A1 B1|
|B2 C2|     |C2 A2|    |A2 B2|

**Ecuación parametrica de la recta L    

x=x0 +  t |B1 C1|    
               |B2 C2|   
y=y0 +  t |C1 A1|    
               |C2 A2|   
z=z0 +  t |A1 B1|    
               |A2 B2|   

Ecuación del haz de planos

Haz de planos: conjunto de planos que pasa por la misma recta

A1x+A2 λx+B1y+B2 λy+C1z+C2 λz+D1+D2 λ=0
n=(A1+A2 λ; B1+B2λ; C1+C2 λ)

Ejercicio

Determinar el angulo entre los planos π1 y π2

Θ= arccos _______(A1.A2+B1.B2+C1.C2)______

               (√A1² + B1² + C1²).(√A2² + B2² + C2²)  

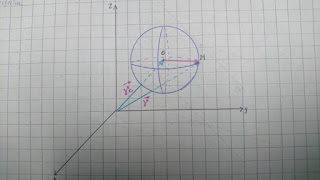
Ecuación de la superficie esférica

**Ec. de la superficie esférica con C(0,0,0) y r=R

(r-r0)=R^2 

**Ec. general de la superficie esférica con C(0,0,0) y r=R

(x-x0)^2 + (y-y0)^2 + (z-z0)^2)=R^2 

Caso particular:

Si C=(0,0,0) --> x^2+y^2+z^2=R^2

Ejercicio

Halle los vectores de los puntos de interseccion de la superficie esferica de ecuacion (R-R0)=R^2 y la recta r=ta.

r1= _____R_____(l,m,n)

      √l² + m² + n² 

r2= - _____R_____(l,m,n)

        √l² + m² + n² 

CILINDROS Y SUPERFICIES CUADRÁTICAS

Análisis gráfico de superficies

1. Intersección de la superficie con los ejes coordenados.
2. Intersección de la superficie con los planos coordenados
3. Intersección de la superficie con planos paralelos a los planos coordenados
4. Bosquejo de la gráfica de la superficie

Referencias:

* Apuntes del cuaderno

*https://sites.google.com/site/avcportafolio/_/rsrc/1427490715467/home/parcial-2/seccion-academica/Captura.JPG